このページでは、IBO(国際バカロレア機構)に掲載されていた、国際バカロレアDPの物理HL(Higher Level)Paper1A 1Bの過去問題(2025年度第1回試験)から抜粋し、日本語に翻訳したものです。
誤訳があるかもしれませんが、テストを受けるための練習になると思いますので、一通りは解くようにしておくと良いと思います。
IB指導実績国内No.1
\ 教師は全員IB経験者の現役大学生 /
受講生の口コミ
教え方が上手くとても分かりやすいです。学校から急な課題を出された際も親身に対応をしてくれます。
指導のためのノートがとてもわかりやすく見やすいです。図式化して教えてくれるので理解しやすい。
日本語で授業させていただいてますが、説明が分かりやすく質問にも丁寧に答えてくれています。
どんな問題も、また進路の相談でも、なんでも即答していただけるので頼りになります。
保護者の口コミ
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
先生の指導のお陰で、IAを終了することが出来ました。娘が大変お世話になりました。
一緒に問題に取り組みながら、子供に寄り添った授業をしていただいています。
※上記はEDUBAL公式サイトより一部引用
\ 初回の体験授業料無料 /
本当に自分に合ったサービスか確認できる
概要
模擬試験
2時間(Paper 1A と Paper 1B)
計算機あり
Paper1A 最高40点
Paper1Aと1B 最高60点
Paper1Aの問題(1〜10)はこちら

問題
1
生徒のグループが、長いひもに吊るされた導電性ボールの運動を調べている。ボールは、電位差 V を持つ2枚の垂直な金属板の間にある。ボールが一方のプレートに接触すると、ボールは帯電し、プレートからはじかれます。与えられた電位差に対して、ボールは一定の周期でプレート間をバウンドする。
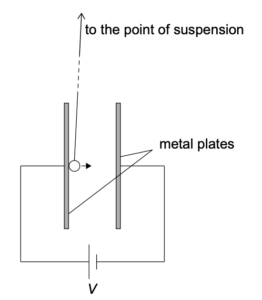
(a)
生徒たちはVを変化させ、ボールが一方のプレートから他方のプレートに1回移動する時間Tを測定する。表はそのデータの一部である。
| $V/kV$ | $T/s\pm 0.1s$ |
| 3.00 | 1.4 |
| 5.00 | 0.8 |
| 7.00 | 0.6 |
(1) Vは直列に接続された2つの同じ電源から供給される。各電源の電位差は、0.01kV の不確かさで既知である。
電位差Vの不確かさを述べよ。

(2) Tは、0.1秒単位で計測できる電子ストップウォッチで計測する。
このストップウォッチを使って、0.1s 未満の T の不確かさをどのように達成できるかを説明しなさい。
グラフはTとVの変化を示している。Vの不確かさはプロットされていない。
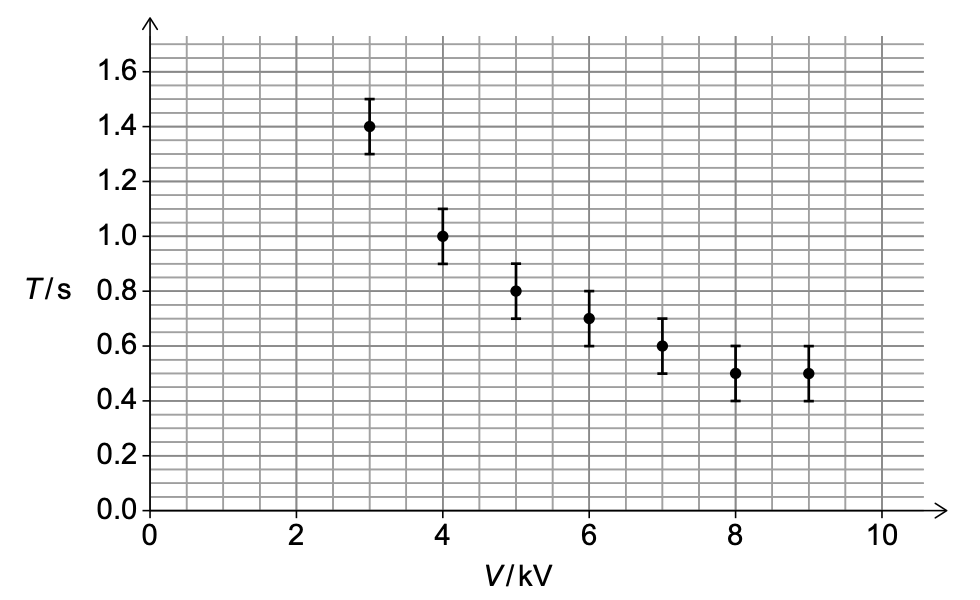
(3) TとVの関係が線形である可能性が低い理由を概説してください。

(4) これらのデータについて、Tの最大の分数不確かさを計算する。

(b)
生徒たちは、TとVの間に次のような理論的関係があることを示唆している
$T=\dfrac{A}{V}$
ここでAは定数である。
この関係を検証するために、Tの$\dfrac{1}{V}$に対する変化をプロットした。
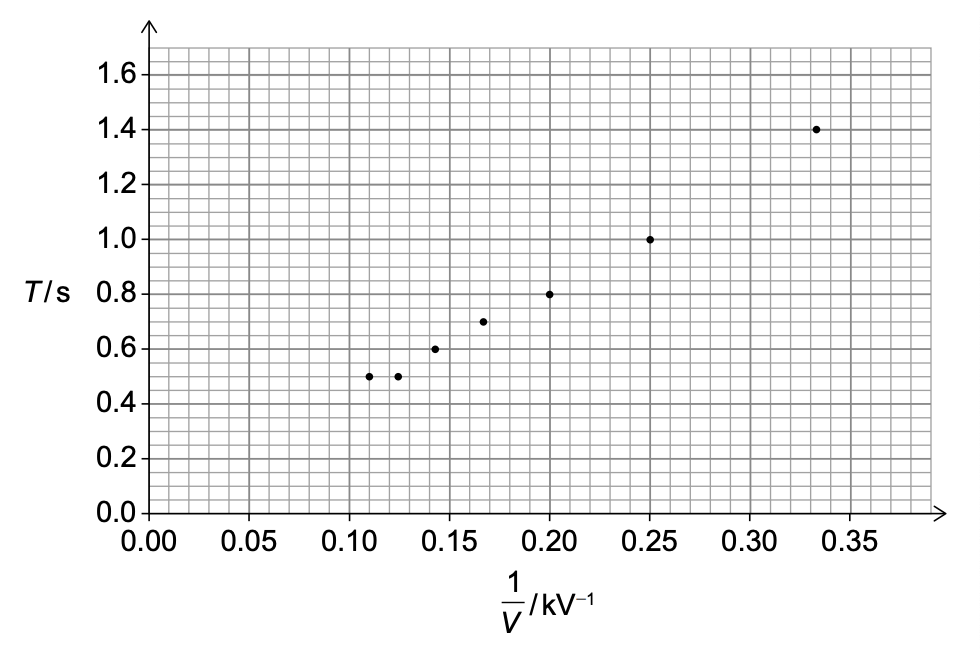
(1) ベストフィットの線を引いてAを決定する。

(2) Aの単位を述べよ。

(3) 理論的な関係は、ボールが電気力によってのみ影響されると仮定している。
この関係をテストするために、ひもの長さをプレート間の距離よりはるかに大きくする必要がある理由を提案しなさい。

2
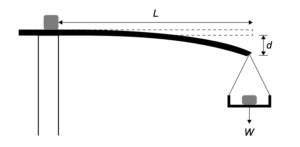
生徒のグループが、一端を水平にクランプしたプラスチックの定規の曲がり具合を調べている。もう一方の端に取り付けたおもりWが定規を曲げます。おもりは計量皿の中に入っている。
生徒たちは定規の長さ L を固定し、W を変化させる。W の各値について、生徒たちはおもり を取り付けた定規の端のたわみ d を測定する。
(a)
このグループは、あるWの値について、dについて次のような繰り返し測定値を得た。
| 1 | 2 | 3 | 4 | 5 | 6 | |
| d / cm | 2.7 | 2.9 | 3.6 | 2.7 | 2.8 | 2.9 |
グループはAとBの2つのサブグループに分かれてデータを分析する。
Aグループはdの平均値を2.93cmと発表。
Bグループはdの平均値を2.8cmとする。
各グループが提示した値について議論しなさい。

(b)
Wによるdの変化を示す。
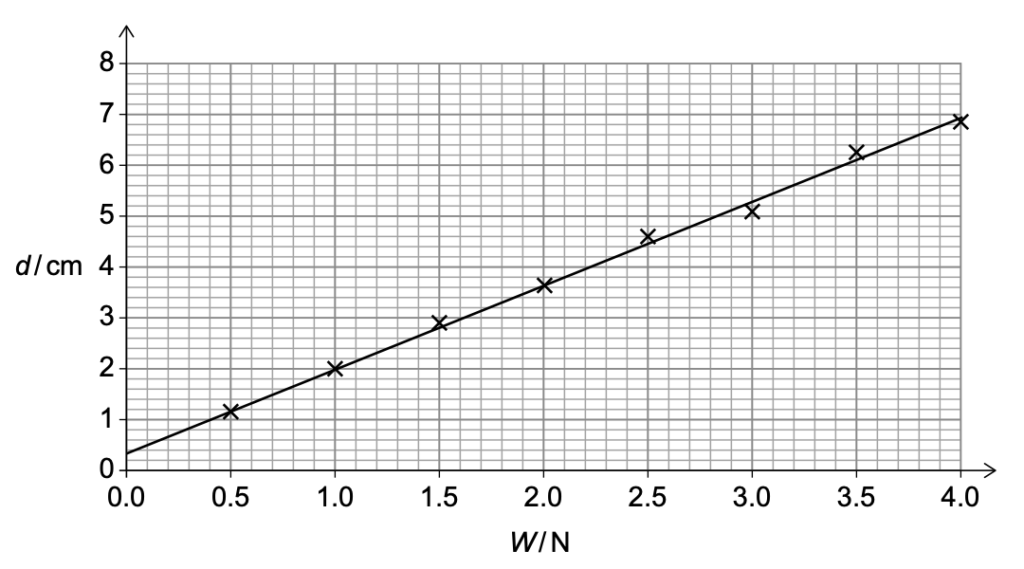
グラフが原点を通らない実験的な理由を1つ概説しなさい。

(c)
理論的には次のように予測される。
$d\propto \dfrac{W^{x}L^{y}}{EI}$
ここでEとIは定数である。Iの基本単位は$m^{4}$であり、Eの基本単位は$kgm^{-1}s^{-2}$ である。
xとyを計算する。

(d)
定規の断面積はA=a×bで、a=(28±1)mm、b=(3.00±0.05)mmである。
(1) bを測定するための適切な測定器を提案する。

(2) Aの値の不確かさのパーセンテージを計算する。

IB指導実績国内No.1
\ 教師は全員IB経験者の現役大学生 /
受講生の口コミ
教え方が上手くとても分かりやすいです。学校から急な課題を出された際も親身に対応をしてくれます。
指導のためのノートがとてもわかりやすく見やすいです。図式化して教えてくれるので理解しやすい。
日本語で授業させていただいてますが、説明が分かりやすく質問にも丁寧に答えてくれています。
どんな問題も、また進路の相談でも、なんでも即答していただけるので頼りになります。
保護者の口コミ
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
先生の指導のお陰で、IAを終了することが出来ました。娘が大変お世話になりました。
一緒に問題に取り組みながら、子供に寄り添った授業をしていただいています。
※上記はEDUBAL公式サイトより一部引用
\ 初回の体験授業料無料 /
本当に自分に合ったサービスか確認できる
解答
1-a
| 答え | ノート | トータル |
| 0.02 «kV» | 1 | |
| 多くのバウンドの時間を測定することによって その結果をバウンス回数で割る | 2 | |
| すべてのエラーバーを直線で結ぶことは不可能である。 | 1 | |
| $T=0.5s$ $\ll \dfrac{0.1}{0.5}=\gg 0.2$ | 2 |
1-b
| 答え | ノート | トータル |
| 1) データの全範囲を通して引かれたベストフィットの直線 半直線より大きな大きな三角形、または半直線より離れた直線上の2つのデータ点 ラインと一致した正しいリードオフ、 例 $\dfrac{1.6-0}{0.40-0}=4.0$ | 3.8~4.2の範囲内の回答を認める。 | 3 |
| 2) kVs | 1 | |
| 3) 弦と垂直の間の角度は、”ボールのどの位置においても “非常に小さくなければならない。 ストリングの張力がボールの重さと “ほぼ “釣り合うように。 or 弦からの復元力/張力の水平成分は “電気力に比べれば “無視できるほど小さい | OWTTE | 2 |
2-a
| 答え | ノート | トータル |
| 3 sfはAには不適切である。 試行3をBの異常値として棄却する。 | 2 |
2-b
| 答え | ノート | トータル |
| 梁が自重で曲がる/鍋の重さで曲がる or dの系統誤差 | 1 |
2-c
| 答え | ノート | トータル |
| $W:kgms^{-2}$ or x=1、y=3を導く仕事 | 2 |
2-d
| 答え | ノート | トータル |
| 1) 測定器(0.05mmまで読み取り可能)の分解能に関連する理由。 | 例:マイクロメーター、スクリューゲージ、バーニアキャリパー、移動顕微鏡 | 1 |
| 2) aまたはbのどちらか[0.0357, 0.0167]の分数の不確かさを計算しようとする。 0.0357 + 0.0167 = 0.05 = 5 % | 2 |
Paper1Aの問題はこちら



