このページでは、IBO(国際バカロレア機構)に掲載されていた、国際バカロレアDPの物理HL(Higher Level)Paper2の過去問題(2025年度第1回試験)から抜粋し、日本語に翻訳したものです。
誤訳があるかもしれませんが、テストを受けるための練習になると思いますので、一通りは解くようにしておくと良いと思います。
IB指導実績国内No.1
\ 教師は全員IB経験者の現役大学生 /
受講生の口コミ
教え方が上手くとても分かりやすいです。学校から急な課題を出された際も親身に対応をしてくれます。
指導のためのノートがとてもわかりやすく見やすいです。図式化して教えてくれるので理解しやすい。
日本語で授業させていただいてますが、説明が分かりやすく質問にも丁寧に答えてくれています。
どんな問題も、また進路の相談でも、なんでも即答していただけるので頼りになります。
保護者の口コミ
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
先生の指導のお陰で、IAを終了することが出来ました。娘が大変お世話になりました。
一緒に問題に取り組みながら、子供に寄り添った授業をしていただいています。
※上記はEDUBAL公式サイトより一部引用
\ 初回の体験授業料無料 /
本当に自分に合ったサービスか確認できる
概要
2時間30分
計算機あり
最高点は90点
物理HL Paper1Aの問題はこちら

物理HL Paper1Bの問題はこちら

問題
1
質量45kgのブロックが水平なテーブルの上に置かれている。ブロックとテーブルの間には摩擦がない。
質量15kgの物体がブロックの上に置かれている。
ブロックに力 F が働き、ブロックは加速する。物体の加速度とブロックの加速度は同じである。
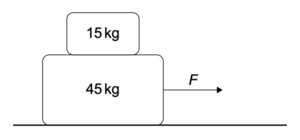
ブロックと物体の間の静止摩擦係数は0.60である。
(a)
15kgの物体を加速させる力の性質と方向を述べよ。

(b)
ブロックと物体が相対的に動かない最大のFの大きさを決定する。

2
ある宇宙船が相対速度0.80cで宇宙ステーションの横を飛んでいる。宇宙ステーションの両端にあるビーコンRとFは、宇宙ステーションの観測者によると同時に光パルスを発している。宇宙ステーションの観測者が測定したところ、パルスは1200m間隔で放出されている。

(a)
速度が0.80cの場合の $\gamma$ を計算しなさい。

(b)
宇宙船の基準フレームについて計算する。
(1) 光パルス間の距離。

(2) 光パルス間の時間。

(c)
どちらの光パルスが先に起こったかを判断する。
3
電子レンジでは電磁波が放射され、オーブン内に定在波パターンが形成される。
平らなチョコレートをオーブン内に置き、マイクロ波のスイッチを入れる。チョコレートは静止している。
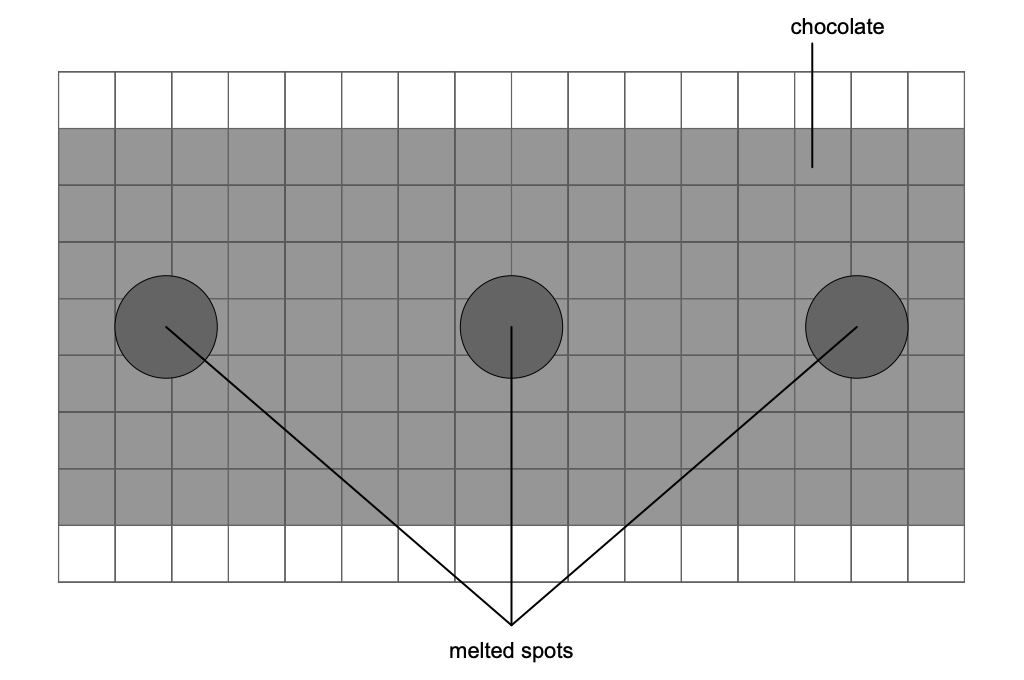
チョコレートの表面に溶けた斑点ができる。図は、チョコレートの融解パターンを示している。それぞれの正方形の長さは1cmである。
(a)
この溶けた斑点の定在波パターンがどのように形成されるかを概説する。

(b)
図から適切な測定を行い、オーブンの電磁波の周波数を決定する。

4
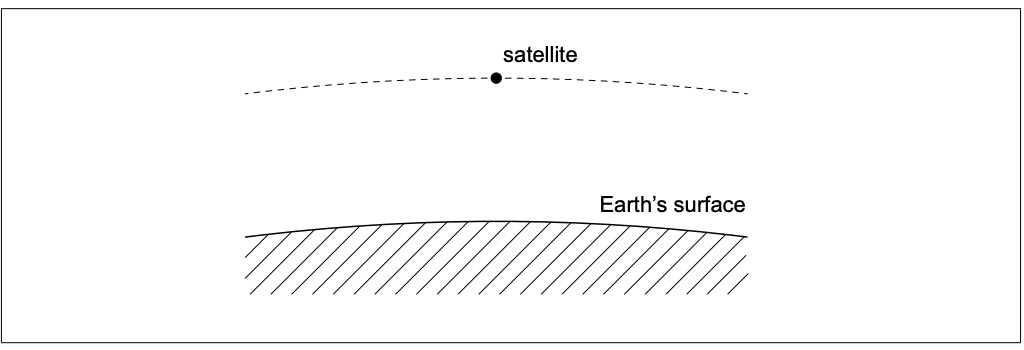
人工衛星は地球の周りを円軌道を描いて回っている。
(a)
図に矢印を描き、衛星の加速度の方向を表す。
衛星の加速方向を表すために、図に矢印を描く。
(b)
以下のデータがある:
地球の質量:$M=5.97\times 10^{24}kg$
地球の半径:$R=6.37\times 10^{6}m$
衛星の軌道周期:$T=5.62\times 10^{3}s$
(1) ケプラーの軌道運動の第三法則では、$T^{2}=kr^{3}$(kは定数、rは衛星の軌道半径)となっている。
$k=\dfrac{4\pi ^{2}}{GM}$であることを示せ。

(2) 衛星の地表からの高さを決定する。

(c)
大気は衛星に小さな粘性抗力を及ぼす。
地球の周りを 1 周する間に、衛星の全エネルギー、運動エネルギー、重力位置エネルギーがどのように変化するかを概説しなさい。

5
2つの導電性リングAとBは、その中心が同じ線上にある。AとBの平面は平行である。リングAは静止しており、リングBは一定の速度でリングAに向かって移動している。
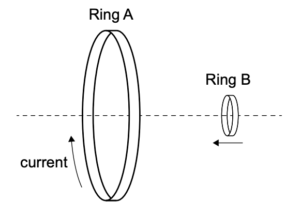
(a)
リングBの磁束が増加する理由を概説してください。

(b)
リングBの誘導電流の方向を述べよ。

(c)
グラフはリングBの磁束の時間変化を示している。
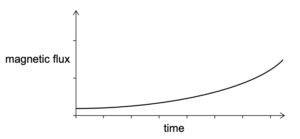
リングBの誘導電流の時間変化について論じなさい。

(d)
リングBが一定の速度でリングAに向かって移動する際に、なぜリングBに仕事をしなければならないのか、その理由を概説する。

6
煙探知機は放射性核種アメリシウム-241を使用する。
アメリシウムは空気に開放されたチャンバー内に収納されている。チャンバー内には2つの電極があり、電源と電流センサーに接続されている。

アメリシウム-241はアルファ粒子を放出し、チャンバー内の空気をイオン化する。各電離は1つのプラスイオンと1つの電子を形成し、これらはイオンペアと呼ばれる。電子とプラスイオンは電極に向かって移動し、センサーは空気中の電流を検出します。
煙がチャンバー内に入ると、形成されるイオン対が少なくなり、センサー内の電流が減少してアラームが鳴ります。
アメリシウム-241の崩壊定数は$5.08\times 10^{-11}s^{-1}$である。
チャンバーの各寸法は0.10m。
(a)
アメリシウム241の原子核は146個の中性子を持っている。この核種はアルファ放出によってネプツニウムに崩壊する。
この崩壊の原子核方程式を完成しなさい。

(b)
放射性線源が住宅内で安全に使用できる理由を概説する。

(c)
検出器の寿命の間に放射性線源を交換する必要があるかどうかを推測する。

線源の初期放射能は42kBqである。この線源から放出されたアルファ粒子の33%がチェンバーに入り、イオン対を形成する。
各アルファ粒子の初期運動エネルギーは5.5MeVである。
1つのイオン対を形成するのに必要なエネルギーは15eVである。
(d)
チャンバー内に煙がないときの、電子によるチャンバー内の最大電流を計算する。

7
$\delta$ VelAは主系列星で、図のような黒体スペクトルを持つ。
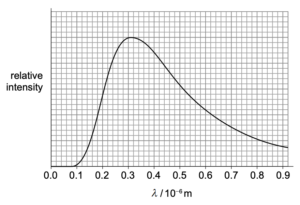
(a)
$\delta$ VelAの表面温度が約9000Kであることを示す。

(b)
$\delta$ Vel Aの見かけの明るさは$2.2\times 10^{-9}Wm^{-2}$で、地球からの距離は$6.2\times 10^{14}km$である。$\delta$ Vel Aの半径を求めよ。

(c)
太陽の半径$R_{\odot }$は$7.0\times 10^{5}km$である。
ヘルツシュプルング・ラッセル線図上に、$\delta$ VelAの位置をスケッチする。
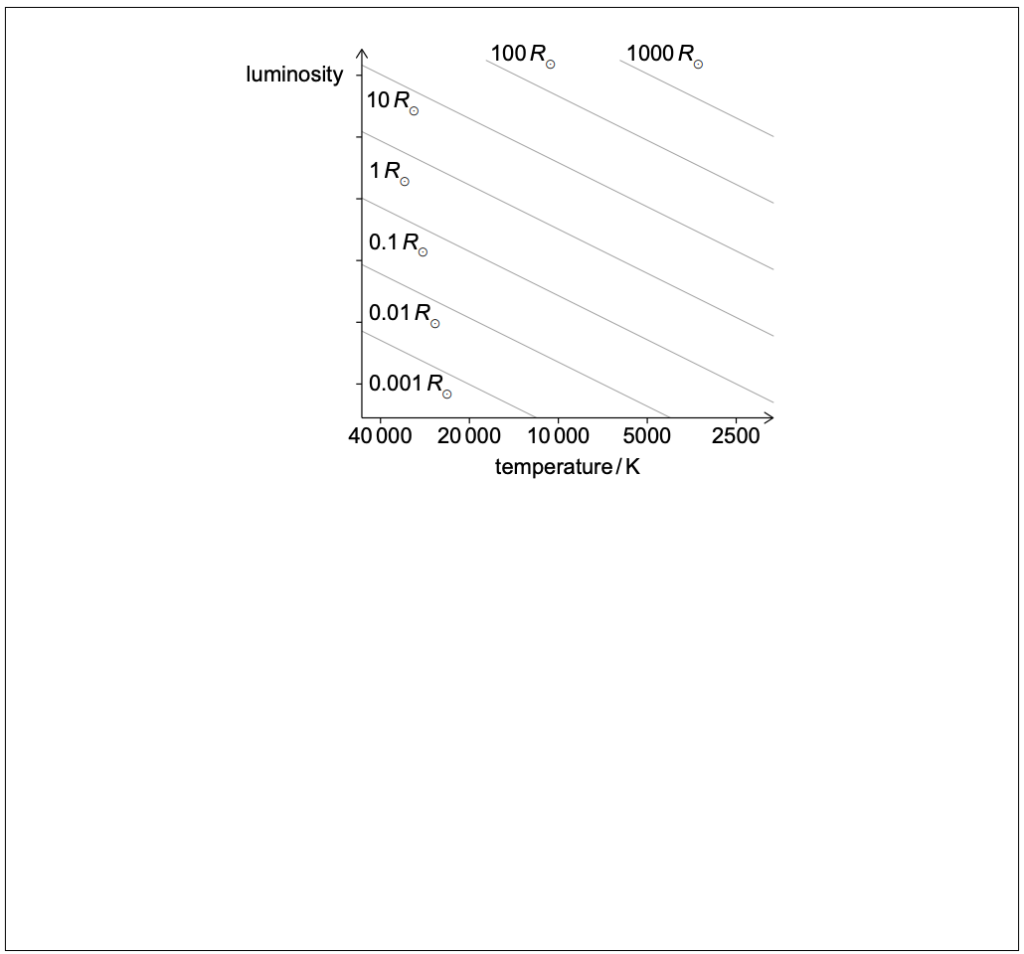
8
温度42℃の総質量30gの固体パラフィンの小片を、温度240℃の液体パラフィン150gと混合する。混合物は平衡温度に達するまで撹拌される。
パラフィンのデータは以下の通り:
固形パラフィンの比熱容量 = $0.7kJkg^{-1}K^{-1}$
液体パラフィンの比熱容量 = $2.13kJkg^{-1}K^{-1}$
パラフィンの比融解潜熱=$220kJkg^{-1}$
パラフィンの融点 = 47℃
a)
混合物の理論平衡温度を計算しなさい。

(b)
(1) 実験を行ったところ、混合物の平衡温度が理論値と異なることがわかった。この違いの理由を考えなさい。

(2) 混合の間、混合物は大きな金属容器に入れられた。(b)(1)の差を小さくするための手順の変更を1つ説明しなさい。

9
この図は、反対に帯電した2枚の平行導電板を示している。
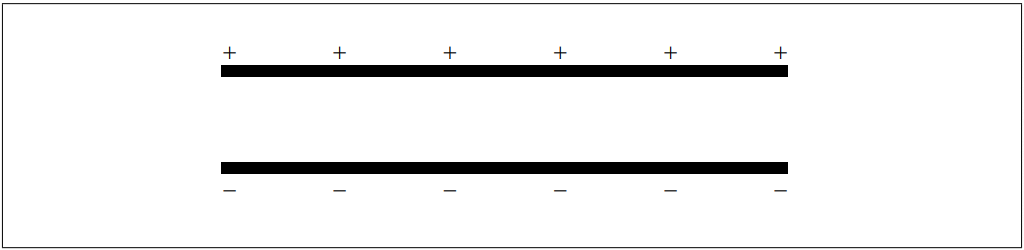
(a)
(1) 帯電したプレートによる電界線を描く。
(2) プレート間の電位差は960Vで、プレート間の距離は8.0mmである。プレート間の電界強度Eを計算しなさい。

実験では、上側のプレートにあけた小さな穴から、プレートとプレートの間に油滴を入れる。油滴はチューブ内の空気中を移動し、プレートの間に落ちる。
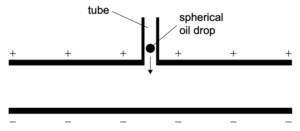
(b)
油滴がチューブを通って落下する際に帯電する理由を説明する。

(c)
油滴はプレートの間の空間に静止しているのが観察される。浮力は液滴に働く力のひとつである。
油の密度は空気の730倍である。
(1) 浮力は重量よりはるかに小さいことを示す。

(2) 浮力を無視して、油滴に働く力を描きなさい。

(3) 油滴の電荷は$q=\dfrac{\rho _{o}gV}{E}$によって与えられることを示せ。
ここで、$\rho_{o}$は油の密度、Vは油滴の体積である。

(4) オイルドロップの電荷の符号を述べよ。

(d)
電場をオフにする。油滴は垂直に落下し、一定の速度vに達する。
(1) この液滴について、$\rho _{o}gV$ = $6\pi \eta$rv($\eta$は空気の粘度、rは油滴の半径)となる理由を概説する。

(2)オイルドロップのチャージが約 $48\times 10^{-19}C$ であることを示す。
オイルドロップのデータは以下の通り:
$r=1.36\mu m$
$\eta =1.60\times 10^{-5}$Pas
$v=0.140mms^{-1}$

(3) 油滴は同じ質量の2つの部分に分かれる。両方とも帯電している。それぞれの部分の正味の電荷を求めよ。

10
物体は、弾性定数 $k$ のバネに吊り下げられて平衡状態にある。物体は、垂直の高さ $h = A$ まで変位し、時間 $t = 0$ で解放され、周期 $T$ の単純調和運動で振動する。
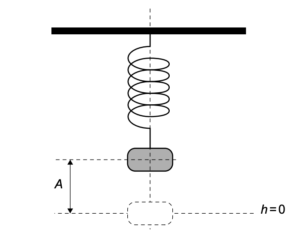
グラフは $t$ による $h$ の変化を示している。
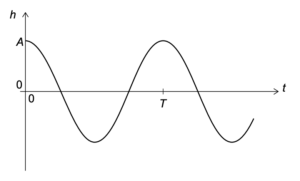
(a)
この振動の運動方程式を述べよ。

(b)
物体の速度 v の t による変化を軸にスケッチしなさい。v 軸上のピーク値に A と T の式で適切なラベルを付ける。

海の波は風によって発生し、電気エネルギーに変換できるエネルギーを運ぶ。海波は、波長l、振幅A、幅wの方形波としてモデル化できる。
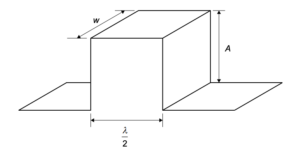
(c)
(1) 図に示された海波の重力ポテンシャルエネルギーは、次のようにモデル化できることを示せ。
$E_{\rho}=\dfrac{1}{4}\rho gw\lambda A^{2}$
ここで $\rho$ は海水の密度である。

(2) 波は速度vで動いている。波から得られる最大パワーはPである。
海の波から得られる波面 $\dfrac{P}{w}$ の単位長さあたりの最大パワーが $\dfrac{1}{2}pqvA^{2}$ である理由を説明しなさい。

熱エネルギーは電気エネルギーの生産にも使われる。熱エネルギーは通常、燃料の化学エネルギーまたは核分裂性元素の核エネルギーから伝達される。
(d)
(1) 燃料を使って熱エネルギーを水に伝え、圧力20MPa、温度550℃の蒸気を発生させる。蒸気はタービン発電システムの羽根を回転させ、最終的に大気圧、温度30℃で凝縮する。
これらの温度間で作動する蒸気タービンの効率が約60%未満でなければならない理由を、熱力学第二法則を参照しながら説明しなさい。

原子炉では、ウラン-235 $( _{92}^{235}U)$ の核分裂による核エネルギーの伝達で水が蒸発する。核分裂は中性子と原子核の衝突によって誘発される。
表は、 $( _{92}^{235}U)$ の核分裂後に燃料棒に存在する一般的な核分裂片の一部である。 元素の記号の後に、陽子番号と核分裂片で観察される核子番号の一部が付されている。
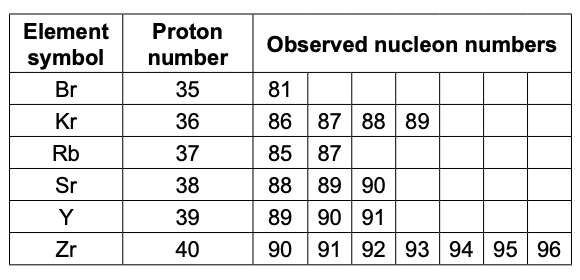
(2) 核分裂では、2つの原子核が数個の中性子とともに生成される。生成物の1つは $( _{56}^{147}Ba)$ 原子核である。
この生成物を持つ核分裂の核反応を述べよ。

平均して、ウラン-235原子の核分裂は200MeVを放出する。石炭のエネルギー密度は約 $25MJKg^{-1}$ である。
(3) 比率の見積もり
$\dfrac{_{}^{235}Uのエネルギー密度}{石炭のエネルギー密度}$

(4) 星のエネルギーは核融合から生まれる。地球上で核融合を利用して大規模に電気エネルギーを供給する試みが研究されている。
これが地球上で実現するための利点と難点を1つずつ挙げなさい。

(e)
この問題では4つのエネルギー生産方法が挙げられている。これらの方法とは、海洋波、石炭、核分裂、核融合である。
これらの方法について論じなさい。
解答では以下の点に言及してください。
- 方法の効率
- 環境への影響
- 資源の利用可能性

IB指導実績国内No.1
\ 教師は全員IB経験者の現役大学生 /
受講生の口コミ
教え方が上手くとても分かりやすいです。学校から急な課題を出された際も親身に対応をしてくれます。
指導のためのノートがとてもわかりやすく見やすいです。図式化して教えてくれるので理解しやすい。
日本語で授業させていただいてますが、説明が分かりやすく質問にも丁寧に答えてくれています。
どんな問題も、また進路の相談でも、なんでも即答していただけるので頼りになります。
保護者の口コミ
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
子供の考えを丁寧に聞いてくださるため、モチベーションが自然と上がっていきます。
先生の指導のお陰で、IAを終了することが出来ました。娘が大変お世話になりました。
一緒に問題に取り組みながら、子供に寄り添った授業をしていただいています。
※上記はEDUBAL公式サイトより一部引用
\ 初回の体験授業料無料 /
本当に自分に合ったサービスか確認できる
解答
・解答欄の各マーキングポイントは、末尾にマークで表示。
・解答欄の括弧内《》の語句は、マークを獲得するために必要な語句ではない。
1
| 答え | ノート | トータル | |
| a | 《ブロック間》の静止摩擦力 AND 右方向 | 1 | |
| b | F = 60a $F_{f}$ = 0.6×15×9.8 《=88.2N》 88.2 = 15×$\dfrac{F}{60}\Rightarrow$F=350《N》 | a=0.6g を使用すると 353N となる。 | 3 |
2
| 答え | ノート | トータル | |
| a | $\gamma =\dfrac{1}{\sqrt{1-0.8}0^{2}}=\dfrac{5}{3}=1.67$ | 1 | |
| b1 | $《\Delta x’=\gamma \left( \Delta x-v\Delta t\right) =》\dfrac{5}{3}\times 1200=2000m$ | 1aからのecfを認める。 $L=\dfrac{L_{0}}{\gamma }$ の使用を認める | 1 |
| b2 | $《\Delta t’=\gamma \left( \Delta t-\dfrac{V}{c^{2}}\Delta x\right) =》\dfrac{5}{3}( 0-\dfrac{0.80}{3\times 10^{8}}\times 1200$) $\Delta t’=《-》5.3《\mu s》$ | $\Delta t=\gamma \Delta t_{0}$の使用を認める | 2 |
| c | なぜなら、$\Delta t'<0$ Fが先 | 2回目のMPは、1回目のMPを正しく解釈した場合のみ与えられる。 | 2 |
3
| 答え | ノート | トータル | |
| a | 定在波は重ね合わせによって《オーブンの中で》形成される / 構成的干渉 エネルギー移動は 《定在波パターンの 》対極で最大になる | 2 | |
| b | $\lambda = 12.2《cm》$ $f《=\dfrac{c}{\lambda }》=\dfrac{3.0\times 10^{8}}{1.22\times 10^{-1}}$ $f$ = 2.46GHz 正解は10の累乗のみ | $\lambda \pm 2mm$ を許容する MP2のみ10乗エラーを容認 | 3 |
4
| 答え | ノート | トータル | |
| a | 地球に向かう軌道に垂直な矢印 | 1 | |
| b1 | $Vorbital=\dfrac{2\pi r}{T}$ と $Vorbital =\sqrt{\dfrac{GM}{r}}$ か $\dfrac{mV^{2}orbita1}{r}=\dfrac{GMm}{r}$ のどちらかを正しく使う $T^{2}=\left[ \dfrac{4\pi ^{2}}{GM}\right] r^{3}$ を得る | $\omega$ の使用を許可する | 1 |
| b2 | $r=\sqrt[3] {\dfrac{GMT^{2}}{4\pi ^{2}}}$ = $t=\sqrt[3]{\dfrac{6.67\times 10^{-11}\times 5.97\times 10^{24}\times \left( 5620\right) ^{2}}{4\pi ^{2}}}$ = $6.83\times 10^{6}《m》$ height = $《6.83\times 10^{6}-6.37\times 10^{6}=》4.6\times 10^{5}《m》$ | 2 | |
| c | 総エネルギーを削減。 したがって、軌道半径の減少は運動エネルギーの増加につながる。 総エネルギーが減少するためには、位置エネルギーの減少が運動エネルギーの増加より大きくなければならない。 | b2からのECFを認める | 3 |
5
| 答え | ノート | トータル | |
| a | リングBは増加する磁力線をカットする。 OR Aの電流による磁場がBの位置で増加する。 | 1 | |
| b | 左巻き | 1 | |
| c | Bの「磁束」の変化率が増加する。 OR グラフの勾配は時間とともに増加する ファラデーの法則では、Bの誘導起電力は《したがって》増加する リングの抵抗は一定なので、誘導電流は増加する | 3 | |
| d | Bに誘導された電流がAの磁場と反対の磁場を発生させる。 OR 運動に対抗する磁力が生じる Bをこの力と反対方向に動かすには、仕事をしなければならない。 | 2 |
6
| 答え | ノート | トータル | |
| a |  | 2 | |
| b | アルファ粒子は空気中を数センチしか飛ばない。 | OWTTE | 1 |
| c | 半減期 $\dfrac{\ln 2}{5.08\times 10^{-11}}≒10^{10}s$ 他の部品の寿命よりはるかに長いという考え 妥当な単位への変換による合理的な比較 例:≒430年 | 3 | |
| d | 各αは $\dfrac{5.5\times 10^{6}}{15}$ = $3.67\times 10^{5}$ のイオン対を生成する。 つまり、毎秒 $\dfrac{3.67\times 10^{5}\times 42000}{3}$ = $5.13\times 10^{9}$ イオンペア。 current = $1.6\times 10^{-19}\times 5.13\times 10^{9}=0.82\times 10^{-9}$ 《A》 | 3 |
7
| 答え | ノート | トータル | |
| a | $\lambda _{\max }=\dfrac{2.9\times 10^{-3}}{T}$ または $9350K$ への正しい置換 | 1 | |
| b | $L=4\pi bd^{2}$ の使用を試みた。 $r=\sqrt{\dfrac{L}{4\pi \sigma T^{4}}}$ の使用。 r = 1.4Gm | 1.3~1.5Gmの範囲を許容する。 | 3 |
| c | $r ≒ 2R\odot$ 図上の正しい位置 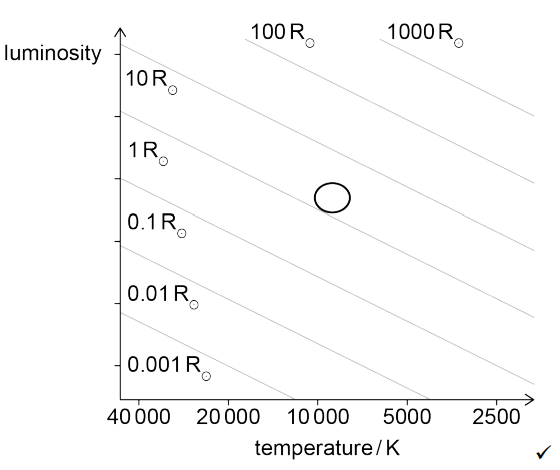 | 9000Kを使用すると $2.2R\odot$ | 2 |
8
| 答え | ノート | トータル | |
| a | $(0.030\times 0.7\times 10^{3}\times 5)$ + $(0.030\times 220\times 10^{3}$ + $(0.030\times 2.13\times 10^{3})(T-47)$ = $(0.150\times 2.13\times 10^{3})(240-T)$ 一つの熱容量項を正しく代入 潜熱を正しく代入 $(0.030\times 220\times 10^{3})$ T = 190《℃》 | 3 | |
| b1 | 実験温度が下がる 環境への熱損失 | 2 | |
| b2 | 容器を断熱する OR 実験を早く行う OR より大量の物質を使う | MAX1 |
9
| 答え | ノート | トータル | |
| a1 | 等間隔に配置された矢印は「目視で」すべて下を向いている エッジエフェクトも矢印で示す | 2 | |
| a2 | $E=\dfrac{V}{d}=\dfrac{960}{8.0\times 10^{-3}}$ $E=1.2\times 10^{5}《NC^{-1}》$ | 2 | |
| b | 摩擦が電子を滴に、あるいは滴から移動させる AND チューブ内の空気分子との衝突・相互作用を通じて、あるいはチューブの壁との衝突・相互作用を通じて。 | 1 | |
| c1 | 油滴の重さは $p_{0}gV$ $\dfrac{F_{b}}{W}=\dfrac{\rho{a}gV}{\rho{o}gV}=\dfrac{\rho_{a}}{\rho_{o}}$ $《\dfrac{F_{b}}{W}=\dfrac{1}{730}=》1.4\times 10^{-3}$ OR FbとWの比は1よりはるかに小さい。 | 3 | |
| c2 | 鉛直下向きの重さと鉛直上向きの電気力 《目測で》で同じ長さ | 2 | |
| c3 | 液滴の質量は $\rho _{o}V$ $qE = (\rho _{0}V)g$ 《hence answer》 | MP1は暗黙的に示さなければならない。 | 2 |
| c4 | Negative | 1 | |
| d1 | 正味の力はゼロ 油滴の加速度はゼロ OR 終端速度のためには、抗力は重量に等しくなければならない。 重力 = $\rho _{o}gV$、抗力 = $6\pi \eta v$ | 2 | |
| d2 | $q=\dfrac{6\pi \eta rv}{E}$ $q=\dfrac{6\pi \times 1.60\times 10^{-5}\times 1.36\times 10^{-6}\times 1.40\times 10^{-4}}{1.2\times 10^{5}}$ $q=4.79\times 10^{-19}《C》$ | 答えは3人以上の観客に見せなければならない。 | 3 |
| d3 | 電荷は量子化される したがって、電荷は1eと2eでなければならない | 2 |
10
| 答え | ノート | トータル | |
| a | h= $A\cos \left( \dfrac{2\pi }{T}t\right)$ OR h= $A\sin \left( \dfrac{2\pi }{T}t+\dfrac{\pi }{2}\right)$ | 説明がない限り、ωやxなどの記号の使用は認めない。 | 1 |
| b | 周期Tの負のサイン曲線 ピーク値を $\dfrac{2\pi A}{T}$ と表記 | 2つ目のマークはωAとする。 | 2 |
| c1 | 1つの頂上の質量を特定する m= $pV=p\dfrac{\lambda }{2}$Aw クレストの重心位置を $\dfrac{A}{2}$ で認識 質量と高さの式を正しく組み合わせた《答えを得るために》。 | 3 | |
| c2 | 波面の単位長さあたりの重力位置エネルギーは $\dfrac{pgw\lambda A^{2}}{4wT}$ = $\dfrac{pgvA^{2}}{4}$ 運動エネルギーは重力位置エネルギーと同じ割合で伝達されるので、合計パワーは $\dfrac{2\rho gvA^{2}}{4}$ となる。 | 2 | |
| d1 | 効率 = 1-$\dfrac{303}{823}$ = 0.63 第二法則は、熱エネルギーから力学的エネルギーへの効率的な伝達の上限を設定する。 | MP1から2sf以上で単位取得。 | 2 |
| d2 | Krが特定 核の方程式は完全に正しい | 右側に2個または3個の中性子があり、質量数が236になる例なら何でも認める。 | 2 |
| d3 | ALTERNATIVE 1 $200\times 10^{6}\times 1.6\times 10^{-19}\times 6.02\times 10^{-23}=1.9\times 10^{13}J$ $\dfrac{1.9\times 10^{13}\times 1000}{235}$ =81TJ ratio = $\dfrac{81\times 10^{12}}{25\times 10^{6}}=3.2\times 10^{6}$ ALTERNATIVE 2 E = 200MeV × e = 3.2 × $10^{-11}J$ $\dfrac{E}{m}=\dfrac{3.2\times 10^{-11}}{235\times 1.67\times 10^{-27}}=8.2\times 10^{13}Jkg ^{-1}$ $\dfrac{8.2\times 10^{13}}{25\times 10^{6}}=3.3\times 10^{6}$ | セカンドM.P.からのecfを許可する。 | 3 |
| d4 | 適切なもの:例えば、放射性断片がなく、容易に核融合可能な元素。 電気的反発を克服するための極端な初期温度、この温度での封じ込め。 | 2 | |
| e | 3マーク 設問で言及された3つの方法すべてを、効率性、環境への影響、資源の利用可能性に言及した適切な概念を用いて、設問中に記述されたいくつかのデータに2度言及し、正しく比較する。 2マーク 設問で挙げられた3つの方法のうち少なくとも2つを正しく比較し、効率性、環境への影響、資源の利用可能性から導き出された2つの適切な概念について、設問のデータに少なくとも1回は言及する。 1マーク 資源の効率性、環境への影響、利用可能性に関連する少なくとも1つの正しい概念に言及し、1つの方法について正しく言及している。 0マーク 一般的なコンセプトで、この問題に特化した正解はなかった。 | 3 |
Paper1Aの問題はこちら



